This a second article in a series dedicated to backtracking algorithms.
Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems which are typically solved using backtracking method have a property in common: These problems can only be solved by trying every possible configuration and each configuration is tried only once.
The rate in a maze statement is as follow:
A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach destination. The rat can move only in two directions: forward and down.
In the maze matrix, 0 means the block is dead end and 1 means the block can be used in the path from source to destination.
Note that this is a simple version of the typical Maze problem. For example, a more complex version can be that the rat can move in 4 directions and a more complex version can be with limited number of moves.
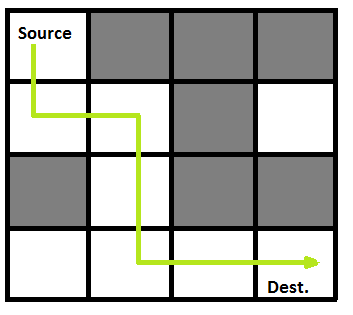
The binary representation of the maze above is as follow:
[
[1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1]
]
The solution matrix (output of program) for the above input matrix is as follow:
[
[1, 0, 0, 0],
[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 1, 1, 1]
]
Algorithm :
If destination is reached
print the solution matrix
Else
a. Mark current cell in the solution matrix
b. Move forward horizontaly and recursively check if this leads to a solution
c. If there is no solution, move down and recursively check if this leads to a solution
d. If none of the above solution work, unmark the cell and return False
Code :
# Utility to check if the current cell position (x,y)
# is in the maze
def isSafe(maze, x, y, sol):
# Get maze dimensions
X = len(maze[1])
Y = len(maze)
if x>=0 and x<X and y>=0 and y<Y and maze[x][y]==1:
return True
return False
# (x,y) is the current cell position
def solveMaze(maze, x, y, sol):
# Get maze size
X = len(maze[1])
Y = len(maze)
# check if (x,y) is goal
if x == X-1 and y == Y-1 :
sol[x][y] = 1
return True
# Check if we're inside the maze
if isSafe(maze, x, y, sol):
# Mark the current cell in solution (BACKTRACK)
sol[x][y] = 1
# Move right
if solveMaze(maze, x+1, y, sol):
return True
# Move down
if solveMaze(maze, x, y+1, sol):
return True
# Remove current cell from solution
# If the 2 moves above failed
sol[x][y] = 0
return False
maze = [
[1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1,]
]
# Initiate the solution matrix
sol = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
# Given a maze NxM,
# we start at (0, 0), goal is (N-1, M-1)
if solveMaze(maze, 0, 0, sol):
print sol
else:
print "No solution"
[[1, 0, 0, 0], [1, 1, 0, 0], [0, 1, 0, 0], [0, 1, 1, 1]]
References:
http://www.geeksforgeeks.org/backttracking-set-2-rat-in-a-maze/