Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. For each move, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap. Nim can be played as a misère game, in which the player who takes the last object loses or as a normal play game, in which the person who makes the last move (i.e., who takes the last object) wins.
In this article, we’ll explore the normal play game.
For example, on a table, there is heaps of stones (or stones or coins) from various sizes. Each player takes one or several stones in a single heap. The winner is the one who can empty the table.

The winning strategy
The following graph represents a game with three heaps containing 1, 2 and 3 stones respectively.
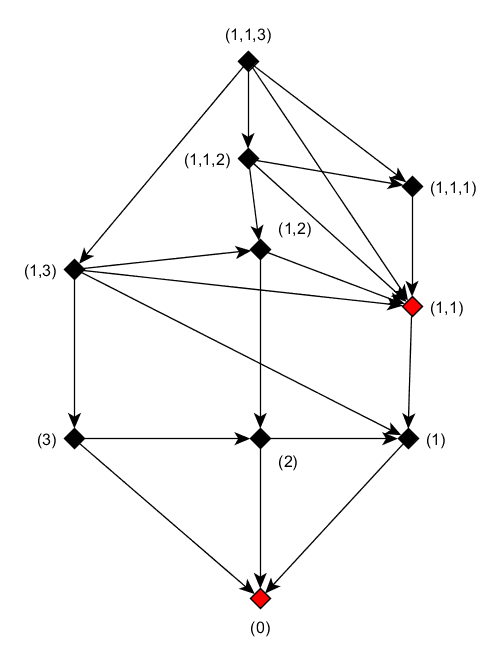
The graph shows the allowed and possible states after a given state.
For example from (1,1,2), the game rule allows the following states (1,1,1) or (1,2) or (1,1), that is from a state of 3 heaps with 1 match in the 1st and second heap and 2 stones in the third heap (1,1,2) , next state could be:
- (1,1,1) 3 heaps with 1 match on each, if the player takes 1 match from the third heap
- (1,2 ) 2 heaps with one and two stones respectively if the player takes 1 match from the first or second heap
- (1,1) 2 heaps with 1 match on each if the player takes the 2 stones of the third heap.
The graph nodes in red compose the graph kernel. The kernel has the following property:
(1) Any node from the kernel can’t have as successor (if it exists) a node from the kernel
(2) Every node out of the kernel has at least one successor, and among them a node of the kernel
A game state or position (or option) can be inside or outside the kernel. The loosing position(s) is inside the kernel (from first property).
Let’s say first position is outside, there is a winning strategy for the first player: step in the kernel (possible, cause of the first property), the second player will step out from the kernel (from the second property). Then the first player will step in the kernel once again, etc. If the first position was inside the kernel, then the second player could adopt the wining strategy of step in, step out the kernel alternatively.
In the context of a finding a winning strategy, properties above can be rewritten as follow:
(1’) From a losing position, all moves lead to a winning position (outside the kernel)
(2’) From a winning position, there is at least one move to a loosing position (in the kernel)
Here comes the first question — under which condition a graph has a kernel ?
We have the Richardson’s theorem which states that every direct graph without an odd cycle has such a kernel, in particular, a graph without a cycle has a kernel and only one. From the game rules, a Nim game’s graph has no cycle, hence a kernel.
Here comes the next question — how to find a graph kernel ?
There is several methods, the must famous one is the binary digital sum.
Determining the graph kernel with XOR
Let’s try to find a way to compute a positive number for each node determining if the node is part of the kernel or not.
Let’s 0, the number assigned to the nodes of the kernel, so any number different from 0 is outside.
Let $x_1, …, x_n$ be the sizes of the heaps before a move, and $y_1, …, y_n$ the corresponding sizes after a move. While respecting the rule of the game (a move is the removal of elements from a single heap $k$), we have $x_i = y_i$ for all $i \ne k$, and $x_k > y_k$ (any move from a position to an other can only change one of the $x_k$).
We have to find an operation ? where, for a given position:
(1’) if $s = x_1 ? … ? x_n = 0$ then all successor positions of this position verifing $t = y_1 ? … ? y_n \ne 0$
(1’) $s = if x_1 ? … ? x_n \ne 0$ then it exists a least a successor position verifying $t = y_1 ? … ? y_n = 0$
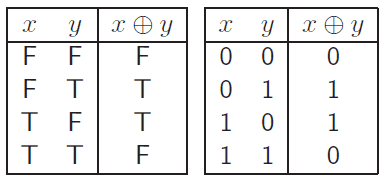
A such operation is the XOR (exclusive or) operation sybolized by $\oplus$.
XOR is a logical bitwise operation, XOR is true only when an odd number of inputs is true. The XOR Truth Table is as follow:
Proof:
Let’s rewrite $x_1, …, x_n$ in base 2.
(1’) : If you change a single bits in a XOR of bits, you’ll change the final result, that is if $s = 0$ then $t \ne 0$
(2’) : From $s \ne 0$, there is at least one way to get a sum t equal to 0 : Let $d$ be the position of the leftmost one bit in $s$ and $k$ a heap where the $d$th bit is also one (it must exist, since $t \ne 0$), then from position d (included), flip all the bits of $x_k$ corresponding to the 1 in the sum s. The new sum s will be 0.
Example : The sum is 01011 (the leftmost nonzero bit is at 2th bit). Using the first heap, flipping the 2nd, 4th and 5th bits:
(d)
(k) 1 1 0 0 1 1 0 0 1 0
0 1 1 1 1 0 1 1 1 1
1 0 0 1 1 1 0 0 1 1
0 0 0 1 1 => 0 0 0 1 1
0 1 1 0 1 0 1 1 0 1
--------- ---------
0 1 0 1 1 0 0 0 0 0
We verify $y_k$ < $x_k$ : all bits to the left of $d$ are the same in $x_k$ and $y_k$, bit d decreases from 1 to 0 (decreasing the value by $2d$), and any change in the remaining bits is of $2^d-1$ at most.
By removing $x_k$ - $y_k$ objects from heap $k$, we get a loosing position for the other player.
From our previous graph, applying XOR on heap sizes, we get the following “nimbers”:
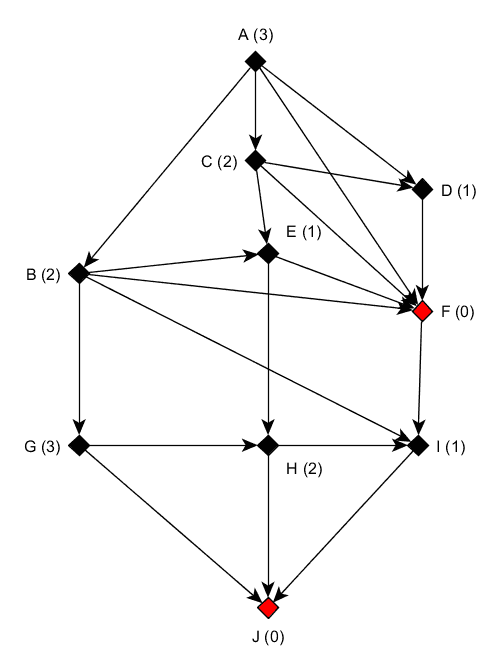
As a conclusion, the winning strategy is to remove stone(s) to leave a game of XOR-sum (aka binary addition) 0 to your opponent.
An example with a game of 3 heaps with size 7, 11, 5 respectively.
Let’s compute the XOR-sum $7 \oplus 11 \oplus 5$:
$7 = 4 + 2 + 1 = 1.2^{2} + 1.2^{1} + 1.2^{0} = 111$
$11 = 8 + 2 + 1 = 1.2^{3} + 0.2^{2} + 1.2^{1} + 1.2^{0} = 1011$
$5 = 4 + 0 + 1 = 1.2^{2} + 0.2^{1} + 1.2^{0}$
Then sum, the base 2 numbers, with 1 + 1 = 0
1 1 1
+ 1 0 1 1
+ 1 0 1
--------
1 0 0 1
$1001 = 1.2^{3} + 0.2^{2} + 0.2^{1} + 1.2^{0} = 9$
To get the 0 sum, let X be the digital sum of all heaps (9 here), find the heap where the XOR-sum of X and heap size is less than heap size (11 here, since $11 \oplus 9 = 2$), then reduce that heap to the XOR-sum of its original size with X (2).
1 1 1
+ 0 1 0
+ 1 0 1
-----
0 0 0
In other word, the winning move is to reduce the size of the 2nd heap to 2 by removing 9 stones.
If you have hard time computing binary addition, just remember there is an easy way to apply the strategy: just leave, whenever possible, a even number of heaps with a number of elements of the powers of 2 (2, 4, 8, 16, etc.).
An other trick is to leave, whenever possible 2 heaps with the same number of elements, this has a XOR-sum of 0, as well. Then, you just have to mimic the moves of your component in the opposite heap to keep the parity of the two heaps.
You’ll find below an implementation of the game where you will never win. The computer always makes a move leaving the board with a XOR-sum of 0 and so always stays outside the kernel. Computer starts (and never starts in a loosing position) so it never looses.
import random
from functools import reduce
def display_board(heaps_):
print('---')
for index, heap_ in enumerate(heaps_):
print('Pile {} : {}'.format(index, 'O ' * heap_))
print('---')
def check_input(heaps_, heap_, stones_):
try:
if stones > heaps_[heap_] or stones_ <= 0 or heap_ > len(heaps_):
raise
except Exception as e:
print(e)
return False
return True
def play(heaps_):
for index, heap_ in enumerate(heaps_):
for j in reversed(range(1, heap_ + 1)):
tmp_heaps = []
tmp_heaps.extend(heaps_[:index])
tmp_heaps.append(heap_ - j)
tmp_heaps.extend(heaps_[index + 1:])
xor = reduce((lambda x, y: x ^ y), tmp_heaps)
if xor == 0:
print('\nMy turn to play : I remove {} stone(s) from pile {}\n'.format(j, index))
return tmp_heaps
# Display game rules
print("""Rules of the game:
I'll build a random board with a random number of piles (between 3 and 6)
and a number of random stones (between 3 and 6) for each piele.
At each move, the player remove stones in one of the pile.
Last player who empties the board wins.
I'll start.
Is here the board:""")
# Build a random board (nb of heaps between 3 and 6, nb of stones between 3 and 6)
nb_heaps = random.choice(range(3, 7))
heaps = []
for i in range(0, nb_heaps):
heaps.append(random.choice(range(3, 7)))
# Cheating... to be sure we never loose.
# We check if the first position is in the kernel. If so, we just removing 1 stone.
if reduce((lambda x, y: x ^ y), heaps) == 0:
heaps[0] = heaps[0] - 1
display_board(heaps)
heaps = play(heaps)
display_board(heaps)
# Go on with the game
while True:
try:
heap = int(input('\nYour turn...\nPick a pile to remove from: '))
stones = int(input('How many stones to remove? '))
except ValueError:
print('\n!!Invalid value, try again!!\n')
if check_input(heaps, heap, stones):
heaps[heap] = heaps[heap] - stones
else:
print('\n!!Invalid value, try again!!\n')
display_board(heaps)
continue
display_board(heaps)
if sum(x == 0 for x in heaps) == len(heaps) - 1:
print('\nI take the last stone(s), you loose...')
break
# Make the opponent enter the kernel
heaps = play(heaps)
display_board(heaps)
References:
Nim on Wikipedia: https://en.wikipedia.org/wiki/Nim
XOR on Wikipedia : https://en.wikipedia.org/wiki/Exclusive_or